[コンプリート！] if u(x y)=x^2+y^2+2x-3xy then 968078

Euler S Theorem On Homogeneous Function

To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `x^3y^33axy=0` then prove that `(d^2y)/(dx^2)=(2a^2x y)/((a xy^2)^3)` Reformulate as a quadratic in a single variable, use the quadratic formula, then reformulate back to find 2x^23xy2y^2 = (2xy)(x2y) If you divide the quadratic through by y^2, then you get (2x^2)/y^2(3xy)/y^2(2y^2)/y^2 = 2(x/y)^23(x/y)2 Let t = x/y and f(t) = 2t^23t2 To factor f(t), find roots of f(t) = 0 using the quadratic formula f(t) = 2t^23t2 is of the form

If u(x y)=x^2+y^2+2x-3xy then

If u(x y)=x^2+y^2+2x-3xy then-For a calculusfree solution, start with the factorization 2x^2 3xy 2y^2 = (x2y)(2xy) and make the substitution u = x2y, v = 2xy Then the condition 25x^2 xy 40y^2 = 36 turnsClick here👆to get an answer to your question ️ If x = 2 and x^2 y^2 3xy = 5 Open in App Solution Verified by Toppr Correct option is B) x 2 y 2 3 x y = If one root of the quadratic equation k x 2 − 3 x − 1 = 0 is 2 1 , then find the value of k Medium View solution > View more CLASSES AND TRENDING CHAPTER

2 Partial Differentiation

 1 If u ( x, y) = x 3 2 x y − 4 x y 2 find the harmonic conjugate v ( x, y) and explain why the function is entire!Click here👆to get an answer to your question ️ If 2x^2 3xy y^2 x 2y 8 = 0 then dydx = Solve Study Textbooks Guides Join / Login Question If u = x 2 3xy y 2 If w(x,y) = xy sin (xy), then prove that ∂^2w/∂y∂x = ∂^2w/∂x∂y asked in Differentials and Partial Derivatives by RamanKumar (501k points) differentials;

 Answer8Stepbystep explanation2(2)^2‒3(2*‒3)‒2(‒3)^22*4‒3(‒6)‒2(9)8‒(‒18)‒118‒16‒1i think it is easy to understand &i hope it will helps you College answered If x = 2 and y = 3, what is the value of 2x^2−3xy−2y^2 HELPPP 1 See answer AdvertisementFactor 2x^2 3xy y^2 and verifyHow do you find the second derivative by implicit differentiation on #x^3y^3=8# ?

If u(x y)=x^2+y^2+2x-3xy thenのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	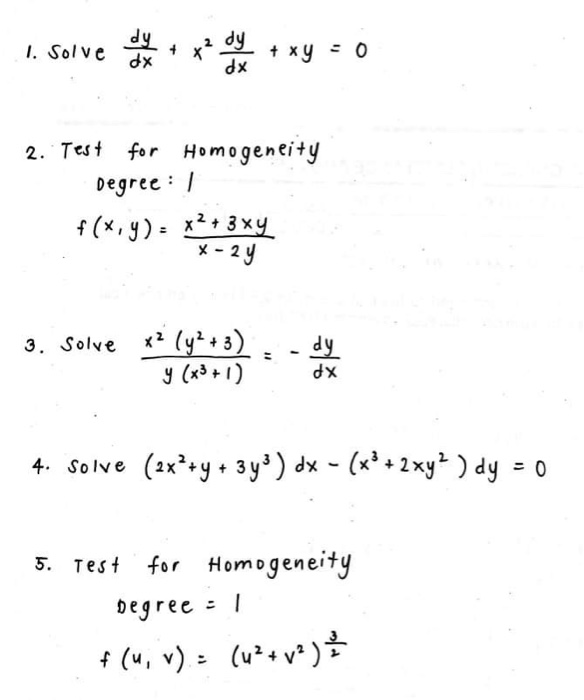2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	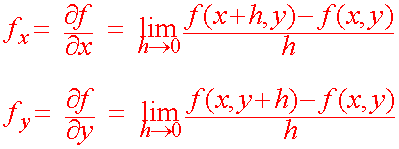2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
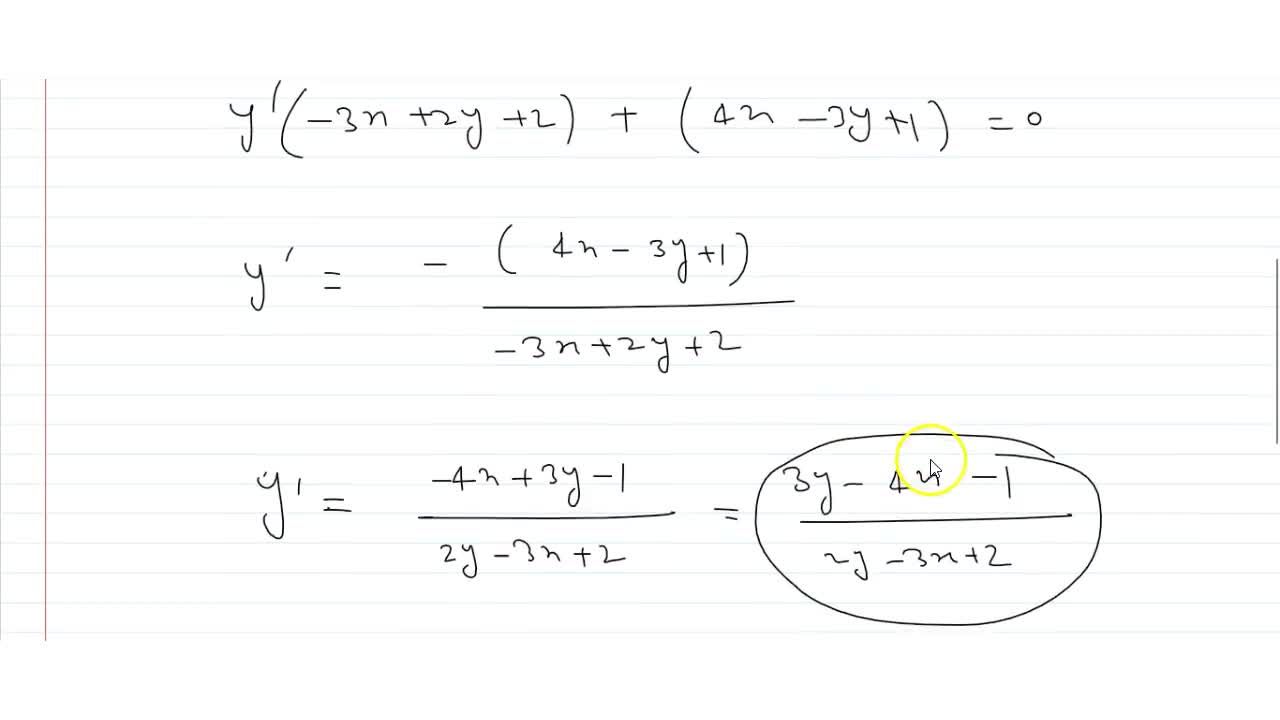2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	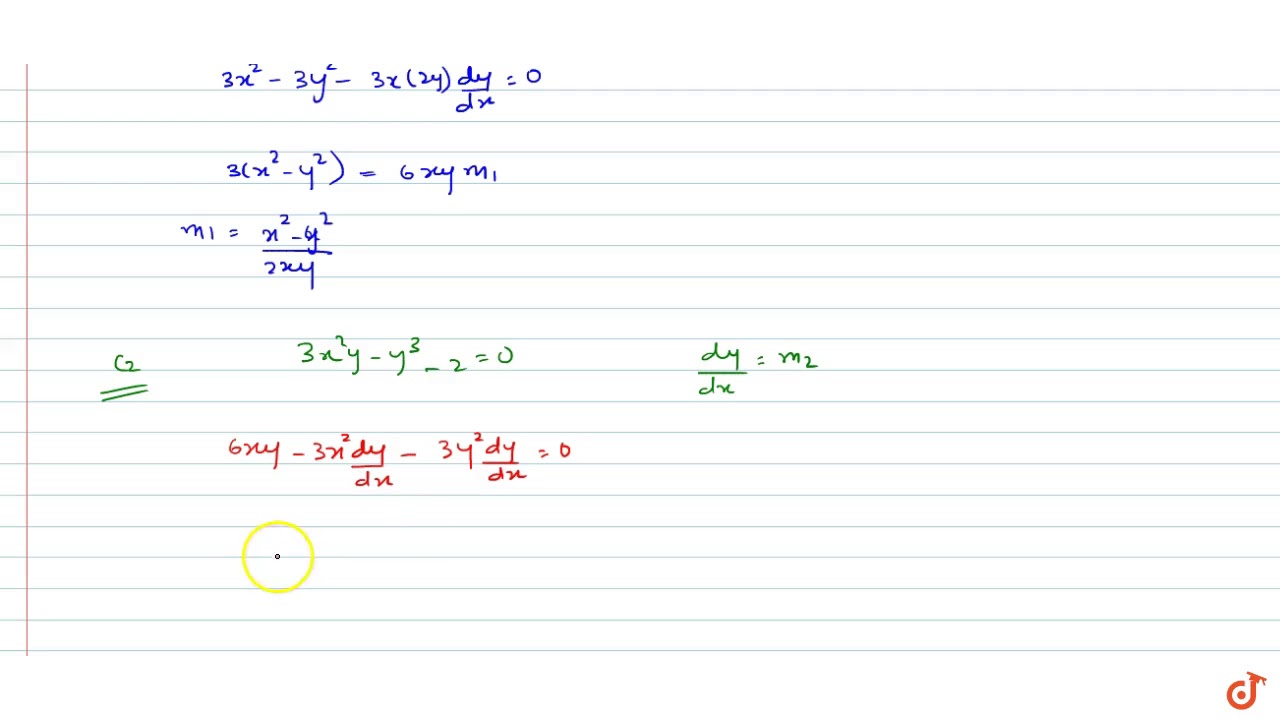2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	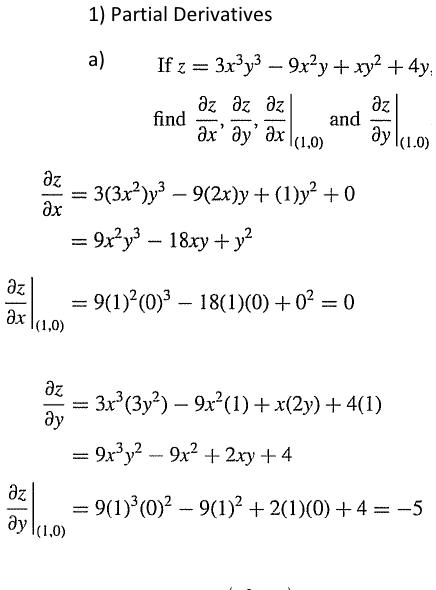2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	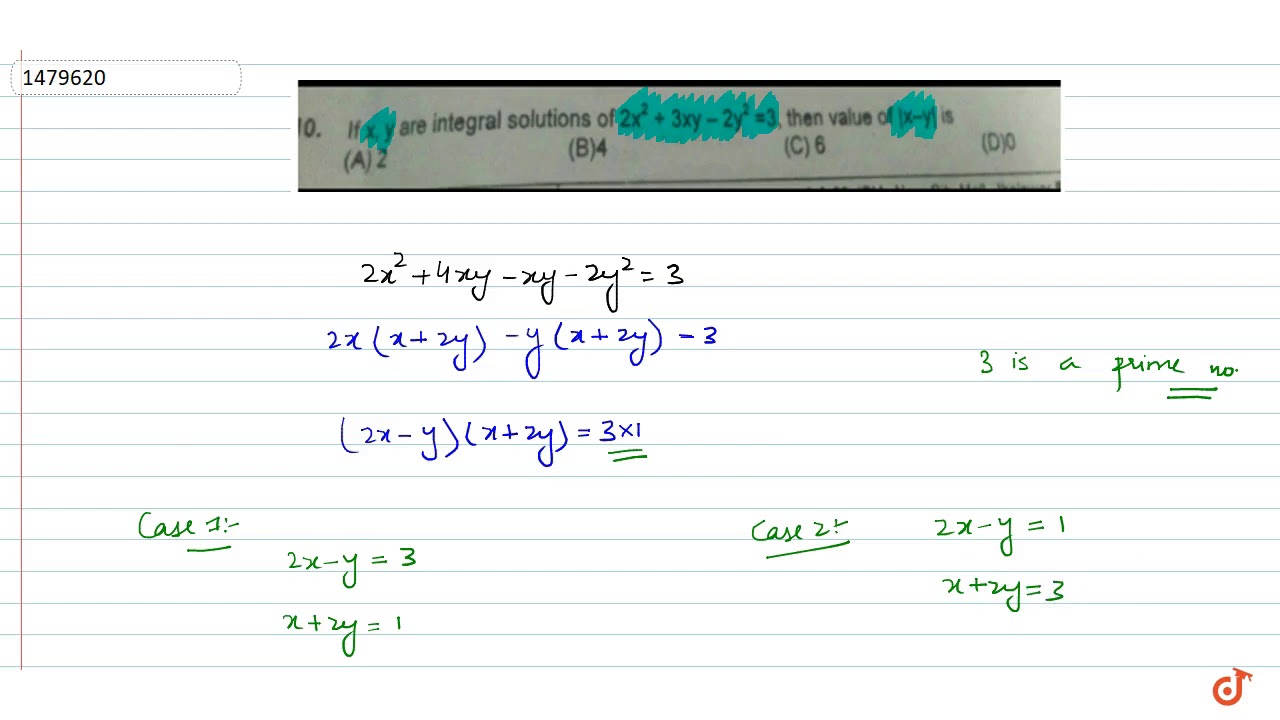2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	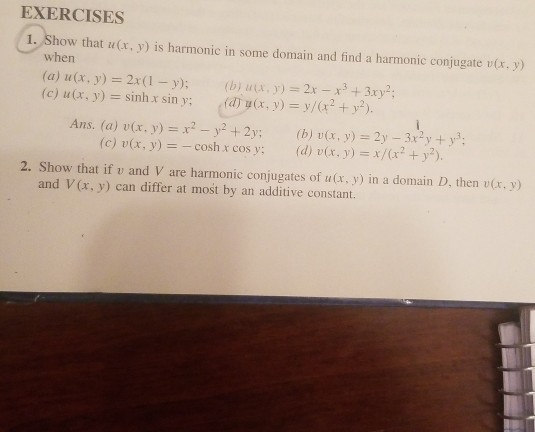2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	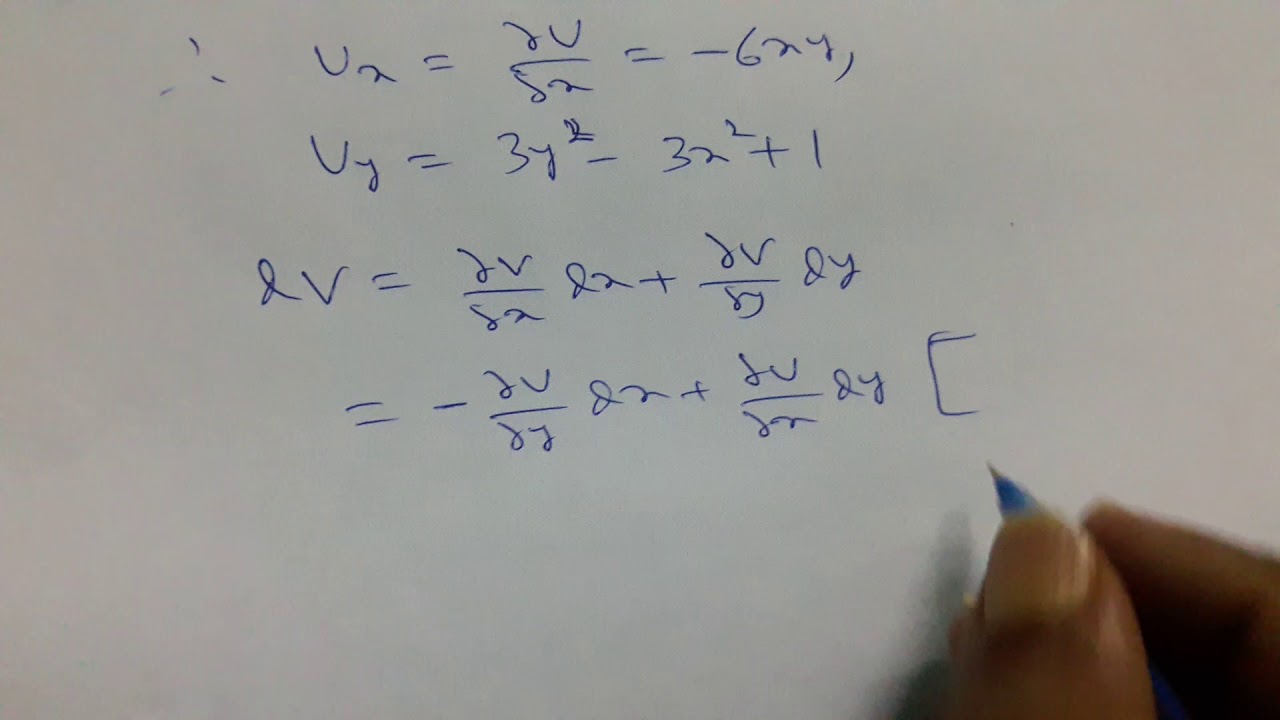2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation	2 Partial Differentiation
2 Partial Differentiation	2 Partial Differentiation

0 votes 1 answer If M = y sin x, then ∂^2u/∂x∂y is equal to (a) cos x (b) cos y (c) sin x By sagemath software, $$\dfrac{du}{dy}=\dfrac{(2xy)u2x^23xy2y^2}{2}=10 \, A^{2} 10 \, A u 25 \, A y$$ This is a first order linear inhomogeneous ODE